2020-01-29

院試対策公式まとめ(微分積分-微分編）

用語
- 微分可能
  
  右微分係数 $y'(a+0) = \lim_{h → +0} \frac{y(a+h) - y(a)}{h}$
  左微分係数 $y'(a-0) = \lim_{h → -0} \frac{y(a+h) - y(a)}{h}$ が一致する時、
  y(t)がt=aで微分可能という。
- 微分作用素（微分演算子)
  
  関数に対して微分操作を作用させることを表す。 $\frac{d}{dx}$ のように表す。
- 連続微分可能
  
  $f^{n}(x)$ が連続であること。そのような関数をまとめて $C^{n}$ 級に属しているとも言える。
- マクローリン展開
  
  $f(x) = f(0) + f'(0)x + \frac{1}{2!} f''(0) x^{2} + \cdots + \frac{1}{n!} f^{(n)}(0) x^{n} + R_{n+1}(x)$
  また、 $R_{n+1}(x) = \frac{1}{(n+1)!} f^{(n+1)}(c) x^{n+1} \quad (0 \lt c \lt x)$
  という表現をラグランジュの剰余項という。 $R_{n+1}(x) = \frac{1}{(n+1)!} f^{(n+1)}(\theta x ) x^{n+1} \quad (0 \lt \theta \lt 1)$ とも表せる。
- ランダウの記号
  
  ある関数f(x)について、 $\lim_{x→0} \frac{f(x)}{x^{n}}$ = 0 の時、
  $f(x) =$ o $(x^{n})$ と表す。
  またx→0として、 $0 \lt |\frac{f(x)}{x^{n}}| \lt M$ (Mはxによらない)となる時、
  $f(x) =$ O $(x^{n})$ と表す。
  これを用いると、 $R_{n+1}(x)$ は o $(x^{n})$ または O $(x^{n+1})$ と表せる。
- テイラー展開
  
  マクローリン展開において0→a x →x-aとおいたもの
  $f(x) = f(a) + f'(a)(x - a) + \frac{1}{2!} f''(a) (x-a)^{2} + \cdots + \frac{1}{n!} f^{(n)}(a) (x-a)^{n} + R_{n+1}(x)$
  $R_{n+1}(x) = \frac{1}{(n+1)!} f^{(n+1)}(a + \theta (x - a) ) (x-a)^{n+1} \quad (0 \lt \theta \lt 1)$
  ランダウの記号を用いると、
  $R_{n+1}(x)$ は o( $(x-a)^{n}$ ) または O ( $(x-a)^{n+1}$ )と表せる。
- テイラー級数
  
  $\lim_{n → ∞} R_n (x) = 0$ なら、
  
  $f(x) = \sum_{k = 0}^{∞} \frac{f^{(k)}(0)} {k!} x^{k}$
  と無限級数の形で表せる。これをマクローリン級数という。
  また、
  $f(x) = \sum_{k = 0}^{∞} \frac{f^{(k)}(a)} {k!} (x-a)^{k}$
  の形をテイラー級数という。
定理
- 定理1 微分操作の線型性
  
  1) $\alpha$ を定数として、 $\frac{d}{dx}$ { $\alpha f(x)$ } $= \alpha \frac{d}{dx} f(x)$
  2) $\frac{d}{dx}$ { $f(x) \pm g(x)$ } $= \frac{df(x)}{dx} \pm \frac{dg(x)}{dx}$
  3) $\frac{d}{dx}$ { $f(x)g(x)$ } = $\frac{df(x)}{dx} g(x)$ + $f(x)\frac{dg(x)}{dx}$
  4) $\frac{d}{dx}$ $\frac{f(x)}{g(x)}$ = $\frac{1}{g^{2} (x)}$ { $\frac{df(x)}{dx} g(x)$ - $f(x)\frac{dg(x)}{dx}$ }
- 定理２　合成関数の微分
  
  合成関数 $y = g(f(x))$ に対して $y = g(z),z=f(x)$ と書くと、
  $\frac{dy}{dx} = \frac{dg(z)}{dz} \frac{df(x)}{dx}$
- 定理3 逆関数の微分
  
  $\frac{df^{-1}(y)}{dy} = \frac{1}{\frac{df(x)}{dx}}$
- 定理4 ライプニッツの公式
  
  $\frac{d^{n}}{dx}$ { $f(x) g(x)$ }= $\sum_{k = 0}^{n}\ _n C_k$ $f^{(k)} g^{(n-k)}$
- 定理5 微分による関数の近似
  
  $f(a+ \Delta x ) \approx f(a) + f'(a) \Delta x$
- 定理6 平均値の定理
  
  関数f(x)が区間[a,b]で連続、(a,b)で微分可能とする。このとき(a,b)上に
  
  $f'(c) = \frac{ f(b) - f(a) }{b - a}$
  となる点cが少なくとも１つ存在する。これを利用すると、
  $f(a + \Delta x) = f(a) + f'(c) \Delta x \quad (a \lt c \lt a + \Delta x)$
  これを拡張すると、Cauchyの平均値の定理が得られる。
  $\frac{ g(b) - g(a) }{f(b)- f(a)} = \frac{ g'(c)}{f'(c)} \quad (a \lt c \lt b)$
- 定理7 ロピタルの公式
  
  f(x),g(x)がx=0の近傍で微分可能であり、 $f(x) \neq 0$ とする。 f(0) = g(0) = 0として $\frac{ g'(c)}{f'(c)}$ のx→0の極限が存在するとき、
  $\lim_{x→0} \frac{ g(x)}{f(x)} = \lim_{x→0} \frac{ g'(x)}{f'(x)}$
- 定理8 ニュートンの方法
  
  f(x) = 0の方程式の解の近似値を求めるときに使える数値解析的方法。 f(x)が[a,b]で下に凸で、f(a) > 0, f(b) < 0,区間内の唯一の解をx=αとする。
  このとき、x=aにおけるy = f(x)の接線とx軸の交点 $a_1$ は、
  $a_1 = a - \frac{f(a)}{f'(a)} \quad (a \lt a_1 \lt \alpha)$
  と表せる。
  $a_{n+1} = a_n - \frac{f(a_n)}{f'(a_n)} \quad (a_n \lt a_{n+1} \lt \alpha)$
  という数列を考えると、αを上界にもつ、単調増加数列となる。 nを大きくしていくと、精度のよい近似解となる。

2020-01-29

院試対策〜線形代数:行列基本編

用語
- 転置行列
  
  $A = a_{ij} \quad$ m×n行列とするとき、
  (i,j)成分が $a_{ji}$ である行列。 $A^{T}$ と表す。
- n次正方行列
  
  (n × n)の行列。　nを正方行列の次数という。
- 正則行列
  
  $XA = AX = E_n$ となるn次正方行列Xをもつn次正方行列A
  このXをAの逆行列といい、 $A^{-1}$ と書く。
  ※逆行列があれば一意である。（存在しない場合もある。）
- 対角行列
  
  　対角成分以外が全て0である行列。
- 対角和
  
  対角成分の和で、 $Tr A = \sum_{a=1}^{n} a_{ii}$ と表す。
- 基本変形
  
  1) ${}$
  $$ P(i;c)= \begin{pmatrix} 1& \\ &\ddots & \\ & & c &\\ & & & \ddots &\\ & & & & 1 \end{pmatrix} $$
  対角成分のうち、(i,i)成分がcで他が1であるような行列。
  この行列を左(右)からかけると第i行(列)目が全てc倍される。
  2) ${}$
  $$ Q(i→j;c)= \begin{pmatrix} 1& \\ &\ddots & \\ & & 1 &\\ & & \vdots & \ddots &\\ & & c & \cdots & 1 & \\ & & & & & \ddots & \\ & & & & & & 1 \end{pmatrix} $$
  全ての対角成分が１で、(j,i)成分がcであるような行列。
  この行列を左(右)からかけると第i行(列)目のc倍が第j行(列)目に加えられる。
  3) ${}$
  $$ I_{ij}= \begin{pmatrix} 1& \\ &\ddots & \\ & & 0 & \cdots & 1 &\\ & & \vdots & \ddots & \vdots &\\ & & 1 & \cdots & 0 & \\ & & & & & \ddots & \\ & & & & & & 1 \end{pmatrix} $$
  対角成分のうち、(i,i)成分と(j,j)成分が0で他が1、(i,j)成分と(j,i)成分が1であるような行列。
  この行列を左(右)からかけると第i行(列)目と第j行(列)目が入れかわる。
  
  1) ~ 3)で左(右)からかける操作を行(列)に関する基本変形という。
  基本変形行列は正則であり、
  $P(i;c)^{-1} = P(i,1/c)$
  $Q(i→j;c)^{-1} = Q(i→j;-c)$
  $I_{ij}^{-1} = I_{ij} \quad$ である。
- 階数(rank)
  
  行に関する基本変形によって単位行列とならずに ${}$
  $$ \begin{pmatrix} 1& \\ &\ddots & \\ & & 1 &\\ & & & 0 & \\ & & & & \ddots &\\ & & & & & 0 \end{pmatrix} $$
  のようにr+1~n行が0になってしまうときのrを行列Aの階数という。どのような基本変形をしても階数は一意。
- エルミート行列（自己随伴行列)
  
  $a_{ij} = \bar{a}_{ji}$ が成り立つ行列のこと。 $A^{\dagger} = A$ と表せる。
  ( $A^{\dagger}$ をAのエルミート共役という。)
  Aの成分が実数であれば、 $A^{T} = A$ となるので、(実)対称行列と呼ぶ。 $(A\boldsymbol{v} , \boldsymbol{u}) = ( \boldsymbol{v}, A^{\dagger} \boldsymbol{u})$ が成り立つ。
- ユニタリ行列
  
  $U U^{\dagger} = E$ を満たす行列U
  Uの成分が実数であるときは、直交行列と呼ぶ。回転行列はユニタリ行列となっている。
正規行列

$A A^{\dagger} = A^{\dagger} A$ を満たす行列A
エルミート行列、ユニタリ行列はともに正規行列
定理
- 定理1 転置行列について
  
  1) $(A^{T})^{T} = A$
  2) $(A + B)^{T} = A^{T} + B^{T}$
  3) $(\alpha A)^{T} = \alpha A^{T} \quad ( \alpha$ は定数)
  4) $(AB)^{T} = B^{T} A^{T}$
- 定理2 行列の区分け
  
  ${}$
  $$
  A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{pmatrix}
  $$
$$ B = \begin{pmatrix} b_{11} & b_{12} & b_{13} & b_{14} \\ b_{21} & b_{22} & b_{23} & b_{24} \\ b_{31} & b_{32} & b_{33} & b_{34} \\ b_{41} & b_{42} & b_{43} & b_{44} \end{pmatrix}
$$

$\quad \quad$ を区切って、

$$ A = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22}
\end{pmatrix}
$$

$$ B = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22}
\end{pmatrix}
$$

$\quad \quad$ とすると、

$$ AB = \begin{pmatrix} A_{11} B_{11} + A_{12} B_{21} & A_{11} B_{12} + A_{12} B_{22} \\ A_{21} B_{11} + A_{22} B_{21} & A_{21} B_{12} + A_{22} B_{22} \end{pmatrix}
$$

$\quad \quad$ が成り立つ。
$\quad \quad$ ※区切りの位置は統一、区切りは増えても良い。
- 定理3 逆行列について
  
  A,Bを実正則行列とする。
  1) $E_n^{-1} = E_n$
  2) $(A^{-1})^{-1} = A$
  3) ABは正則行列であり、 $(AB)^{-1} = B^{-1} A^{-1}$
- 定理4
  
  A,Bを正方行列、P,Qをn次正則行列とし、B = PAQ
  この時、Aが正則であることと、Bが正則であることは同値
- 定理5
  
  $$ A = \begin{pmatrix} a_1 & \\ & a_2& \\ & & \ddots &\\ & & & a_n \end{pmatrix} B = \begin{pmatrix} b_1 & \\ & b_2& \\ & & \ddots &\\ & & & b_n \end{pmatrix} $$
  とすると、
  $$ AB= \begin{pmatrix} a_1 b_1& \\ & a_2 b_2& \\ & & \ddots &\\ & & & a_n b_n \end{pmatrix} $$
  $$ A^{-1}= \begin{pmatrix} a_1^{-1}& \\ & a_2^{-1}& \\ & & \ddots &\\ & & & a_n^{-1} \end{pmatrix} $$
- 定理6 逆行列の存在の必要十分条件
  
  n次正方行列Aに逆行列が存在する　 $\Longleftrightarrow$ Aの階数がn
- 定理7 ユニタリ変換の内積不変
  
  Uをユニタリ行列とし、 $x' = Ux \quad y' = Uy$ とすると、
  
  $( x' , y' ) = (x ,y )$
- 定理8 ユニタリ行列の性質
  
  1) A,Bをn次ユニタリ行列とすると、AB,BAはn次ユニタリ行列
  2)n次単位行列は、n次ユニタリ行列
  3) Aがユニタリ行列なら、逆行列が存在し、逆行列もユニタリ行列

2020-01-21

院試対策公式まとめ(微分積分-関数編）

用語
- 逆正弦
  
  $x = siny$ を $y$ について解いたものを $y=arcsinx$ と表す。
- 逆余弦
  
  $x = cosy$ を $y$ について解いたものを $y=arccosx$ と表す。
- 主値
  
  逆正弦、逆余弦は $y$ について解くと答えが一つに定まらない。
  そのうち $-1 \leq x \leq 1$ に対し、逆正弦では $- \frac{\pi}{2} \leq y \leq \frac{\pi}{2}$ 、逆余弦では、 $０ \leq y \leq \pi$
- 双曲線関数
  
  $sinhx = \frac{e^{x} - e^{-x}}{2} \quad$ $coshx = \frac{e^{x} + e^{-x}}{2} \quad$ $tanhx = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$
  
  $cosh^{2} x - sinh^{2}x = 1 \quad$ $1 - tanh^{2} x = \frac{1}{cosh^{2}x}$ が成り立つ。
- 符号関数
  
  ${}$ $$ sgn(x) = \left\{ \begin{array}{} -1 & ( x < 0) \\ 1 & ( x > 0) \end{array} \right. $$
- 陰関数
  
  F(x,y) = 0 のような形で表される関数
  一方、y = F(x)のような形の関数を陽関数という。
- 代数関数
  
  $R_0(x),R_1(x) \dots R_n(x)$ をxの多項式とした時の陰関数
  $F(x,y) = R_n(x) y^{n} + \cdots + R_0(x) = 0$
  で定まる関数のこと。
- 左極限
  
  $\lim_{x \to {a - 0}}f(x) = b$ $\Longleftrightarrow$
  
  $\forall ε > 0$ $\quad \exists$ $\delta > 0 \quad$ $s.t. \quad a - \delta \lt x \lt a \quad$ $\Longrightarrow$ $\quad |f(x) - b| \lt \varepsilon$
- 右極限
  
  $\lim_{x \to {a + 0}}f(x) = b$ $\Longleftrightarrow$
  
  $\forall ε > 0$ $\quad \exists$ $\delta > 0 \quad$ $s.t. \quad a \lt x \lt a + \delta \quad$ $\Longrightarrow$ $\quad |f(x) - b| \lt \varepsilon$
  
  左極限と右極限が一致すると $\lim_{x \to {a}}f(x) = b$
- 関数の連続性
  
  $f(x)$ が点 $x = a$ で連続　 $\Longleftrightarrow$
  
  $\forall ε > 0$ $\quad \exists$ $\delta > 0 \quad$ $s.t. \quad |x-a| \lt \delta \quad$ $\Longrightarrow$ $\quad |f(x) - b| \lt \varepsilon$
- 偶関数
  
  $f(-x) = f(x)$ を満たす関数
- 奇関数
  
  $f(-x) = -f(x)$ を満たす関数
  
  $f(x) = \frac{f(x) + f(-x)}{2} + \frac{f(x) - f(-x)}{2}$ と分解すると、第１項が偶関数、第２項が奇関数と分解ができ、これは一意である。
- 凸関数
  
  定義域内の任意の２点x,yと0 < λ < 1 を満たす任意の実数λに対し、
  $f((1-\lambda)x + \lambda y) \leq (1 - \lambda)f(x) + \lambda f(y)$
  
  が常に成り立つ関数

定理
- 定理2.1
  
  1) $\lim_{x \to {a + 0}}$ { $f(x) + g(x)$ } = $\lim_{x \to {a + 0}}f(x)$ + $\lim_{x \to {a + 0}}g(x)$
  
  2) $\lim_{x \to {a + 0}}f(x)g(x)$ = $\lim_{x \to {a + 0}}f(x)$ ・ $\lim_{x \to {a + 0}}g(x)$
  
  3) $\lim_{x \to {a + 0}} \frac{f(x)}{g(x)}$ = $\frac{\lim_{x \to {a + 0}}f(x)}{\lim_{x \to {a + 0}}g(x)}$
  
  なお、左極限、両方からの極限でも成り立つ。
- 定理2.2
  
  $f(x),g(x)$ が点 $x = a$ で連続だとすると、
  $f(x) + g(x), f(x)g(x)$ も $x = a$ で連続、 $g(a) \neq 0$ なら、
  $\frac{f(x)}{g(x)}$ も $x= a$ で連続。
  また、 $h(x) = g( f(x) )$ という合成関数があるとき、
  $f(x)$ が $x = a$ で、 $g(x)$ が $x = f(a)$ で連続ならば、
  $h(x)$ は $x = a$ で連続である。
- 定理2.3
  
  $f(x)$ が点 $a$ で連続になるためには、 $a$ に近づくどんな数列 $a_n$ に対しても、 $n \rightarrow$ ∞ の時、 $f(a_n) \rightarrow a$ となっていることが必要十分条件
- 定理2.4 中間値の定理
  
  閉区間[ $a,b$ ]で連続な関数 $f(x)$ は、この区間で $f(a)$ と $f(b)$ の中間の任意の値Cをとる。　　
- 定理2.5 最大値の定理
  
  閉区間[ $a,b$ ]で連続な関数 $f(x)$ は、この区間で最大値をとる。
  以下の1),2)を用いて証明される。
  
  1) ある定数Mが存在して、閉区間[ $a,b$ ]で連続な関数 $f(x)$ は、
  
  $\quad a \leq x \leq b$ において $\quad f(x) \leq M$
  
  上式が成り立つ最小のMを区間[ $a,b$ ]上でのfの値の上限といい、
  
  $sup_{a \leq x \leq b} f(x)$
  
  と表す。 2) 連続関数が閉区間[ $a,b$ ]で取る値には上限が含まれる。

2020-01-20

院試対策公式まとめ(微分積分-数列・極限編）

用語
- 三角不等式
  
  $|a + b | \leq | a | + | b |$
  $|a - b | \geq |a| - |b|$
- 収束の定義
  
  $\forall ε > 0$ $\quad \exists$ $n_\varepsilon \quad$ $s.t. \quad n \geq n_\varepsilon \quad$ $\Longrightarrow$ $\quad |a_n - a| \lt \varepsilon$
  
  このとき、 $\lim_{n \to \infty} a_n = a$
- Cauchy列
  
  $\forall ε > 0$ $\quad \exists$ $n_\varepsilon \quad$ $s.t. \quad m,n \geq n_\varepsilon \quad$ $\Longrightarrow$ $\quad |a_m - a_n| \lt \varepsilon$
  を満たす数列
- 上限,下限
  
  数の集合Aについて上界の中で最小のものを上限といい、sup Aと書く。下界の中で最大のものを下限といい、inf Aと書く。
- 実数の連続性の公理
  
  実数全体の集合 $\boldsymbol{R}$ において、上に有界な任意の部分集合Aをとったとき、Aの上限sup Aが $\boldsymbol{R}$ の中に存在する。
- 交代級数
  
  $a_n > 0$ として、
  
  $\sum_{n = 1}^{∞} (-1)^{n-1} a_n$ $\quad = \quad a_1 - a_2 + a_3 - \cdots$
  
  の形で表される級数
- 絶対収束
  
  $\lim_{n \to \infty}|a_n|$ < ∞
  級数が絶対収束すれば、もとの級数も収束する。
- 条件収束
  
  　ある級数が、絶対収束はしないが、収束すること。
- 各点収束
  
  関数列 $f_1 (x), f_2 (x), \cdots , f_n (x), \cdots$ を考える。 $f_n (x)$ が区間[a,b]の全ての点でf(x)に収束するとき、つまり、
  
  $\lim_{n → ∞} f_n (x) = f(x)$
  が成り立つとき、関数列は区間[a,b]で各点収束するという。
- 一様収束
  
  任意の $\epsilon \gt 0$ に対して、xに無関係にεだけで決まる番号Nが存在して、n>Nとなるすべてのnについて $| f_n (x) - f(x) | \lt \epsilon$ となるとき、関数列 $f_1 (x), f_2 (x), \cdots , f_n (x), \cdots$ はf(x)に一様収束するという。
- 関数級数
  
  $\sum_{n = 1}^{∞} f_n (x) = f_1 (x) + f_2 (x) + \cdots$ を関数級数という。この部分和 $S_N (x)$ がS(x)に一様収束するとき、関数級数は一様収束するという。
- べき級数
  
  $\sum_{n = 0}^{∞} a_n x^{n} = a_0 + a_1 x + a_2 x^{2} + \cdots$ の形で表される級数のこと。
- 収束半径
  
  $\sum_{n = 0}^{∞} a_n x^{n}$ がx = cで収束するようなcの値の集合を考えその上限をRとしたとき、Rをべき級数の収束半径という。|x| < R となるxに対して $\sum_{n = 0}^{∞} a_n x^{n}$ は絶対収束する。
  収束半径Rのべき級数 $\sum_{n = 0}^{∞} a_n x^{n}$ は以下の性質を持つ。
  1) |x| > R のとき、発散.
  2) |x| < Rでは、絶対収束。また0<Rの時、0<ρ<Rとなるρについて|x|≤ρで一様収束.
  3) R=0のとき、x=0の場合のみ収束.
  4) R=∞のとき、すべてのxに対して収束.
  なお、|x| = Rに関しては不定
  収束半径は、 $R = \lim_{n → ∞} | \frac{a_n}{ a_{n+1} } |$ で与えられる。
定理
- 定理1 （有界単調列の収束）
  
  実数の列{ $a_n$ }が単調に増加し、かつ上に有界であるならば、{ $a_n$ }はある実数 $a$ に収束する。
- 定理2 アルキメデスの原理
  
  任意の正の実数a,bに対して、na > bとなる自然数nが存在する。
- 定理3 区間縮小法
  
  ２つの数列{ $a_n$ }と{ $b_n$ }が、
  
  $a_1 \leq a_2 \leq \cdots \leq a_n \leq \cdots \leq b_n \leq \cdots \leq b_2 \leq b_1$
  を満たし、 $\lim_{n → ∞} ( b_n - a_n ) = 0$ が成り立つなら、
  
  $\lim_{n → ∞} a_n = \lim_{n → ∞} b_n = a$
  となる１つの実数aが存在する。
- 定理4 ボルツァノ-ワイエルシュトラスの定理
  
  有界な数列{ $a_n$ }は収束する部分列をもつ。
- 定理5 $\quad a_n, b_n$ が収束すれば、
  
  1) $\lim_{n \to \infty} (a_n + b_n) = \lim_{n \to \infty}a_n + \lim_{n \to \infty}b_n$
  
  2) $\lim_{n \to \infty} (a_n b_n) = \lim_{n \to \infty}a_n ・ \lim_{n \to \infty}b_n$
  
  3) $\lim_{n \to \infty} \frac{a_n}{ b_n}= \frac{\lim_{n \to \infty}a_n}{\lim_{n \to \infty}b_n }$
- 定理6
  
  1) deg p は多項式pの次数を表すとする。
  deg p > deg q ならば $\lim_{n \to \infty} \frac{q(n)}{p(n)} = 0$
  
  2) $\lim_{n \to \infty}\frac{n^{k}}{a^{n}} = 0 \quad( k > 0, a > 1)$
  
  3) $\lim_{n \to \infty}\frac{a^{n}}{n!} = 0 \quad(a > 1)$
  
  4) $\lim_{n \to \infty}$ ${\sqrt[n]{n}}= 1$
- 定理7
  
  $a_n$ が単調減少して0に収束していれば、交代級数は収束する。
  またこの級数を第n項で切ったときの部分和の誤差は、 $a_{n+1}$ で抑えられる。
- 定理10 はさみうちの原理
  
  $\lim_{n \to \infty} a_n$ = $\lim_{n \to \infty} b_n = a$ 、
  かつ大きなnに対して $a_n \leq c_n \leq b_n$ が成り立つとき、
  $\lim_{n \to \infty} c_n = a$ が成り立つ。
- 定理8 Cauchyの判定条件
  
  無限級数 $\lim_{n \to \infty} a_n$ が収束するための必要十分条件は、
  $\forall ε > 0$ に対し、nを十分に大きく取れば、 $\forall p \geq 0$ に対して、
  $| \sum_{k = n}^{n + p} a_k |$ < ε
  が成り立つこと。
- 定理9 コーシーの定理
  
  数列{ $a_n$ }が収束するための必要十分条件は、{ $a_n$ }がコーシー列になることである。
- 定理10 級数に関するコーシーの定理
  
  級数 $\sum_{n = 1}^{∞} a_n$ が収束するための必要十分条件は、
  
  $\forall ε > 0$ $\quad \exists$ $n_0 \quad$ $s.t. \quad m \gt n \geq n_0$ $\Longrightarrow$ $|a_{n+1} + a_{n+2} + \cdots + a_{m} | \lt \varepsilon$
  
  が成立することである。
- 定理11
  
  正項級数 $\sum_{n = 1}^{∞} a_n$ が収束するための必要十分条件は、部分和の数列{ $S_n$ }が有界となることがある。
- 定理12
  
  2つの正項級数 $\sum_{n = 1}^{∞} a_n$ , $\sum_{n = 1}^{∞} b_n$ に対して、 $a_n \leq K b_n$ (Kは正の定数) が成り立つとき、 $\sum_{n = 1}^{∞} b_n$ が収束すれば、 $\sum_{n = 1}^{∞} a_n$ は収束する。また、 $\sum_{n = 1}^{∞} a_n$ が発散すれば $\sum_{n = 1}^{∞} b_n$ も発散する。
- 定理13
  
  2つの正項級数 $\sum_{n = 1}^{∞} a_n$ , $\sum_{n = 1}^{∞} b_n$ に対して、
  
  $\lim_{n → ∞} \frac{a_n}{b_n} = K$
  となる正定数Kが存在するとき、 $\sum_{n = 1}^{∞} b_n$ が収束(発散)すれば $\sum_{n = 1}^{∞} a_n$ も収束(発散)する。
- 定理14 ダランベールの判定法
  
  正項級数 $\sum_{n = 1}^{∞} a_n$ において、
  
  $\lim_{n → ∞} \frac{a_{n+1}}{a_n} = r$
  のとき、r<1なら $\sum_{n = 1}^{∞} a_n$ は収束し、r>1なら $\sum_{n = 1}^{∞} a_n$ は発散する。
- 定理15 コーシーの判定法
  
  正項級数 $\sum_{n = 1}^{∞} a_n$ において、
  
  $\lim_{n → ∞} a_n^{\frac{1}{n}}= r$
  のとき、r<1なら $\sum_{n = 1}^{∞} a_n$ は収束し、r>1なら $\sum_{n = 1}^{∞} a_n$ は発散する。
- 定理16
  
  区間[a,b]における連続関数列 $f_n (x)$ が関数f(x)に一様収束するとき、
  1) f(x)は連続関数となる。
  2) 極限と積分は交換できる。つまり、
  
  $\lim_{n → ∞} \int_{a}^{b} f_n (x) dx = \int_{a}^{b} f(x) dx$
- 定理17
  
  区間[a,b]における連続関数列 $f_n (x)$ が関数f(x)に各点収束し、さらに $f'_n (x)$ が連続でg(x)に一様収束するとき、 $g(x) = f' (x)$ が成り立つ。
- 定理18
  
  区間[a,b]における連続関数列 $f_n (x)$ が $\sum_{n = 1}^{∞} f_n (x)$ がS(x)に一様収束するとき、
  1) S(x)は連続関数となる。
  2) $\int_{a}^{b} S(x)dx = \int_{a}^{b} f_1(x)dx + \int_{a}^{b} f_2(x)dx + \cdots$
- 定理19
  
  区間[a,b]において $f_1(x) + f_2(x) + \cdots$ がS(x)に各点収束し、 $f'_{1} (x) + f'_{2} (x) + \cdots$ の各項が連続で,T(x)に一様収束するとき、S(x)は微分可能であり、S'(x) = T(x)が成り立つ。
- 定理20 ワイエルシュトラスの優級数判定法
  
  区間[a,b]における関数列 $f_n (x)$ が,区間内のすべてのxに対して、
  $| f_n (x) | \leq M_n$
  が成り立ち、正項級数 $\sum_{n = 1}^{∞} M_n$ が収束するとき、関数級数 $\sum_{n = 1}^{∞} f_n (x)$ は一様収束する。

2020-01-09

EfficientNet

イントロ

これまでの畳み込みネットワークでは、層を深くしたり、幅を広げたり、解像度を上げたりと、どれか１つの要素を増やすことで精度を上げてきた。この論文では、畳み込みネットワークの改良について再考し、上記３要素をバランスよく増やして精度を上げる方法を提案している。

複合スケーリング

畳み込みネットワークNは以下のような式で表すことができる。

f:id:Becon147:20191220132048p:plain — ネットワークの定式

なお、
X:入力
H,W:解像度
C:チャンネル数
F:畳み込み層などのオペレータ
添字i:ステージ番号
L:ステージ内の繰り返し回数　である。各ステージは同じ畳み込み層を用い、L回繰り返す。

複合スケーリングではF自体は変えず、（つまり畳み込み層の形状を変えず）L,C,H,Wを増やしていく。さらに設計空間を減らすために、これらすべてを一定の割合で増やしていく。
そのために以下のように問題を再定式する。

f:id:Becon147:20191220133246p:plain — 問題の再定式

w,d,rはスケーリングの係数である。最適なw,d,rを求めるために難点となるのは、互いに依存しており、資源の制約によって値が変わってきてしまうことである。このような難点のため、これまでは一つの要素についてスケーリングしていた。

f:id:Becon147:20191220133839p:plain — w,d,rのみでスケーリングした時のFLOPSとImageNetにおける精度

上図は、w,d,rのみでスケーリングした時の関係図である。
wを大きくすると、きめ細かい特徴が捉えられ、学習しやすくなる。しかし、幅があって浅いネットワークでは高レベルの特徴を捉えるのは難しくなってしまう。
dを大きくすると、複雑な特徴なども取り扱え、他のタスクにも応用しやすくなる。しかし、勾配消失問題の影響で学習が難しくなってしまう。
rを大きくすると、潜在的にきめ細かい特徴が捉えられるが、それだけ層を深くしたり幅を広げたりする必要がある。

またいづれの係数も大きくしていくと、大きなモデルになってしまい、FLOPSの上昇に対する精度の上昇がかなり小さくなってしまうという難点がある。

f:id:Becon147:20191220142010p:plain — wを変化させた時のFLOPSとImageNetにおける精度

上図をみると、wを変化させた時の精度の上昇は、dとrに大きく影響を受けていることがわかる。このことから、w,d,rのバランスがとても重要であることがわかった。

先行研究では、ランダムにパラメータをチューニングしていたが、本論文では、複合スケーリング法を提案する。

f:id:Becon147:20200108222319p:plain — 複合スケーリング法

φは、どれだけモデルスケーリングに資源を用いることができるかによって、ユーザ指定で操作できる変数であり、α、β、γは深さ、幅、解像度にどれだけ資源を割り当てるかを指定する変数である。(α、β、γはグリッドサーチによって決定する。）

EfficientNetの構造

モデルスケーリングでは層の構造を変えることができないので、良いベースラインを用いることが重要である。今回ベースラインとして提案するのがEfficientNetである。以下がその構造である。

f:id:Becon147:20200108230214p:plain — EfficientNet-B0の構造

MnasNetと類似しているが、目標FLOPSが400Mと少し大きいため、少し大きな構造となっている。

このEfficientNet-B0をもとに複合スケーリング法を用いてモデルを拡張していく。まずφを１に固定し、グリッドサーチによりα、β、γを決定する。最適なパラメータは、α＝1.2、β＝1.1、γ＝1.15となった。
次にα、β、γを固定し、Φを徐々に大きくしていく。これにより、EfficientNet-B1~B7を得る。

グリッドサーチはそれぞれのモデルで行なった方が良い精度を期待できるが、モデルが大きいため多大なサーチコストがかかることが予想される。そのため、小さなモデルでのみグリッドサーチを行う。

実験結果

f:id:Becon147:20200108232839p:plain — ImageNetにおける精度とFLOPS

上図を見ると。これまでの代表的な畳み込みネットワークと比較すると、少ないパラメータ数、FLOPSでより良い精度を足していることがわかる。

また、実際のハードウェア上においてこれまでのネットワークよりも（例ではGPipe)高速学習となっている。

転移学習においてもこれまでの畳み込みネットワークと比較して、少ないパラメータ数で、同等またはそれ以上の精度を発揮している。

ディスカッション

f:id:Becon147:20200109094241p:plain — 単一要素のスケールアップと複合スケーリング法

上図を見ると、深さ、幅、解像度のみをスケールアップしていくよりも、複合スケーリング法を用いてスケールアップしていく方が有用であることがわかる。

2019-12-17

Wide Residual Networks

ResNetを改良したWide Residual Networksを紹介した論文を英訳し、まとめてみた。
- 元論文
Wide Residual Networks

イントロ

CNNは年々層数が増えていき、多くの分野で利用されている。しかし、ネットワークが深いと勾配発散、消失など様々な問題が発生してしまう。

そのような状況の中、提案されたResNetはresidualモジュールを用いた手法で上記のような問題を解決した。さらにResNetブロックの中身の改良や、層を深くする研究が行われてきた。

ResNetブロックでは、ショートカットとして恒等写像を利用している。恒等写像を利用することで、パラメータを少なくすることができるなど、様々なメリットがある。その反面、いくつかのブロックしか有用にならなかったり、多くのブロックがあっても各ブロックが少しの情報量しか持たないというデメリットもある。

本論文では、層を深くするのではなく、各層の幅を広げるという違う観点でネットワークを改良し、その有用性を調べた。

Wide Residual Networkの要素

ResNetとは、下のようなresidualモジュールを用いたネットワークであり、これをもとにしている。式で表すと、 $x_{l+1}=x_l+F(x_l)$ となる。なお、下図ではF(x)が２つの畳み込み層を表している。

f:id:Becon147:20191217204523p:plain — Residualモジュール

基本構造では、３×３の畳み込み層を直列につなげている部分を改良して、trainの速さ、精度などを調査していく。小さいフィルターが効率的であることがわかっているので、今回は３×３より大きいフィルターは使用しない。本論文では以下の部分を変化させている。

residualブロックの形

residualモジュール内の畳み込み層の数やカーネルのサイズをB(a,b,c)のように表す。例えば、基本構造ではB(3,3)となっている。
residualブロックの畳み込み層の数

　lを各ブロック内の畳み込み層の数を表している。例えば、基本構造ではl=2となっている。
residualブロックの幅

今回のネットワークの肝である、ブロックの幅をkで表す。例えば、基本構造ではk=1となっている。なおk=1のネットワークをthin、k＞1のネットワークをwideと呼ぶこととする。

これらを調節してできたネットワークを WRN-n-k-B(M)と表す。なお、nは畳み込み層の総数を表している。

DropOutの有用性

Dropoutとは、ニューラルネットワークの学習時に一定確率でノードを不活性化することで、過学習、共適応を避けるための手法である。
現在では、Batch Normalizationに置き換えれており、Dropoutを利用するよりも精度が良いという研究結果が出ている。

本研究では、層の幅を広げることでパラメータ数が多くなってしまうため、dropoutを採用する。先行研究で、恒等写像の部分に用いると悪影響であることが示されているので、畳み込み層の部分に導入した。

実験結果

実験では、データセットとしてCIFAR-10を利用している。

ブロック内の畳み込みの形式比較

ネットワークはWRN-40-2を利用する。ただし、パラメータ数を同じぐらいにするために、B(3,3)ではWRN-28-2,B(3,1,3)では、WRN-22-2を用いた。
ブロック内の畳み込み形式による比較
上図を見ると、(3,3),(3,1),(3,1,3)が有効であることが,パラメータ数が同数であればそれほど差異はない。
ブロック内の畳み込み層数の比較

ネットワークはWRN-40-2を利用し、畳み込み層は全て３×３を用いる。パラメータ数は同程度になるように調整する。
ブロック内の畳み込み数による比較
上図より、B(3,3)が最適であることがわかる。 B(3,3,3),B(3,3,3,3)が劣化するのは、residual connectionが減ってしまうからだと考えられる。
ブロックの幅による比較

ブロックの幅による比較
層の深さを固定して、幅を広げると精度が上がる。
一方で幅を固定して層を深くすると、depth=28までは精度が上がっていたが、depth=40になると精度が下がってしまった。

f:id:Becon147:20191214124730p:plain — 他のCNNとの比較

他のCNNと比較すると、WRNsが有効であった。よってオリジナルのResNetの層の深さと幅の比は適切ではないことがわかる。

Dropoutの使用有無

Dropoutの使用有無の比較
パラメータ数が多い層では効果を発揮しており、正則化の手法として有効であることが示された。これはthin(k=1),wide(k>1)いづれでも有効であった。

f:id:Becon147:20191214132232p:plain — dropoutの有無とtraining lossとtest errorの推移

また、上図のようにResidualネットワークでは、急激にエラー率が上昇することがある。しかし、dropoutを用いるとそのような現象が解消していることがわかる。

計算効率

wideとthinのネットワークのtrain時間の比較
上図が示すように、thin(l=1)のネットワークよりもwide(l>1)のネットワークの方が、明らかに速いことがわかる。

結論

Wide Residual Networksは、同等のパラメータ数を持つResNetよりも効率的であり、精度も高かった。このことからresidual networkの重要な部分は、極端に深いネットワークではなく、residualブロックであるということがわかった。

2019-12-12

Resnet論文 (Deep Residual Learning for Image Recognition)要約

論文和訳 ResNet CNN 機械学習

現在、CNNを用いた画像認識手法はたくさんあるが、その中でResNetは様々な手法のもととなっている。そこでこのResNetを解説した論文
Deep Residual Learning for Image Recognition を和訳し、まとめてみた。
(訳ミス、捉え間違いなどあればご指摘していただけると幸いです🙇‍♂️）

イントロ

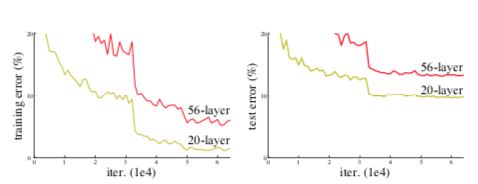
これまでの実験からネットワークの深さは、精度に大きく影響する。しかしながら、層を深くすればいいというわけではない。
勾配爆発、消失の問題が発生し、学習が進まない可能性があるからである。
⇨これまでは初期値を標準化し、標準化層を挿入することでこの問題を解決してきた。

このような勾配消失は、過学習によって起こるものではなく、層を追加することにより学習誤差も大きくなる。

f:id:Becon147:20191212222400p:plain — 左:ベースラインのネットワーク　右:ResNet

→全てのネットワークが簡単に最適化できるわけではない。

この論文で提案するのはresidualモジュールである。

residualモジュールとは、入力をxとすると、普通の層による処理F(x)と恒等写像xを足し合わせたものを次の出力H(x)とするモジュールである。
式で表すと、 $H(x) = F(x)+x$ となる。

residualモジュール

先ほど説明したように、入力をxとすると、H(x) = F(x)+xを出力とするモジュールである。
図で表すと以下のようになる。

f:id:Becon147:20191212224122p:plain — Residual モジュール

F(x)としては様々な関数を選択することができる。ただし、1層のみではあまり長所を生かせないので、2層以上にするのが一般的である。例では、1つの層の後にReLU、さらに1つの層という構造である。

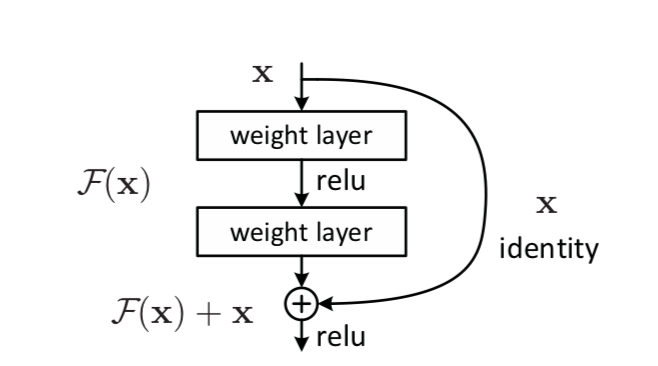
これは、入力と出力の次元が一致する必要がある。一致しない場合は以下の式適用する。

$H(x)=F(x)+W_sx \tag{1}$

$W_s$ は次元を一致させるための行列である。

ResNet

ベースラインは、以下の写真中央のようなものである。
f:id:Becon147:20191212222554p:plain

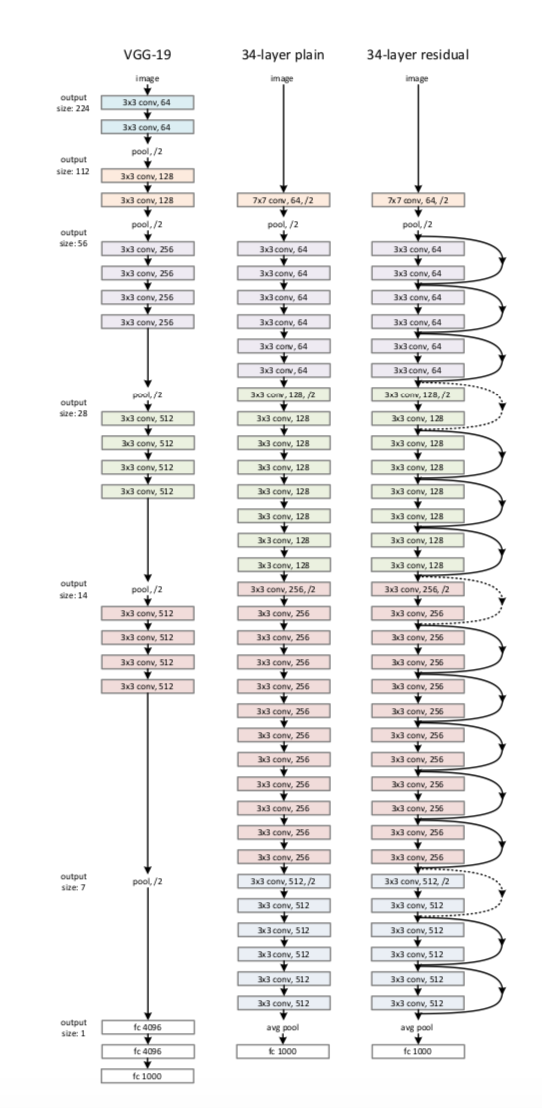
ほとんどは3×3の畳み込み層である。
各層は同じ数のフィルタを持ち、特徴マップのサイズが半分になったら、フィルタの数を2倍にする。(ストライドを2にする)
最後に平均プーリング層、全結合層に通し、ソフトマックスを用いて出力する。

これをベースに、写真右のようにresidualモジュールを導入する。
フィルタの数が2倍になる時は、0をpaddingするか(2)式を利用する。

これは34層なのでResNet-34となる。

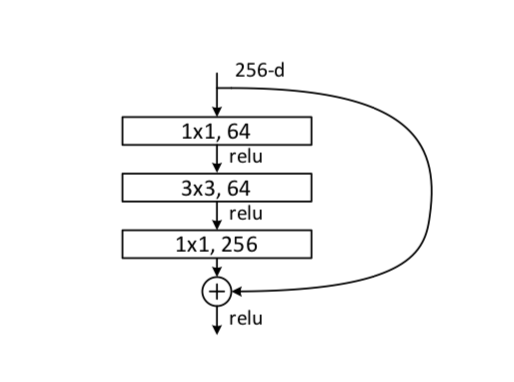
ボトルネック構造

上記のResNetでは、F(x)として２層の畳み込みを利用している。これを修正したものがボトルネック構造である。F(x)として、１×１、３×３、１×１の畳み込み層を用いている。図で表すと下のようになる。

f:id:Becon147:20191212232019p:plain — ボトルネック構造

この構造では、パラメータがないことが効果的となっており、ResNet-50,101,152などにおいて使われている。

実験

事件ではImageNet 2012 classificationのデータセットを用いている。
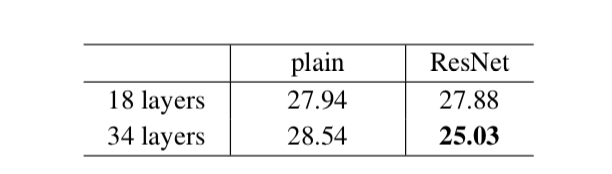
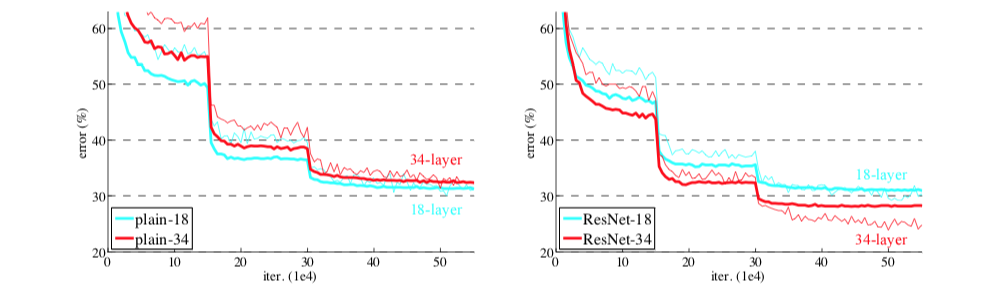
ベースラインのネットワーク(plain)を用いると、層の数を増やしたとき、エラー率が高くなってしまう。
ResNetを用いると、この現象が改善し、同じ層の数を用いた場合、ベースラインよりも精度が上がっている。また収束速度も速くなっている。

f:id:Becon147:20191212222855p:plain — ImageNetにおけるエラー率

f:id:Becon147:20191212225631p:plain — ベースライン(plain)と、ResNetのエラー率

ショートカットには3通りの方法がある。
A:次元変化の時に0-paddingを用い、パラメータはない。
B: 射影と恒等写像を組み合わせて用いる。
C: 射影のみ用いる。

下図のようにA<B<Cと性能が良くなるが、それに従ってパラメータ数も増えることから、射影を用いる重要性はあまりない。
また、パラメータが少ない方がボトルネック構造において効果的である。 ⇨恒等写像(xそのまま)をショートカットにする。

他のデータセットに対しても、効果を発揮しており、物体認識のタスクにおいても使うことができる。

用語

微分可能

微分作用素（微分演算子)

連続微分可能

ランダウの記号

テイラー級数

定理

定理1 微分操作の線型性

定理２ 合成関数の微分

定理3 逆関数の微分

定理4 ライプニッツの公式

定理5 微分による関数の近似

定理6 平均値の定理

定理7 ロピタルの公式

定理8 ニュートンの方法

用語

転置行列

n次正方行列

対角行列

対角和

階数(rank)

エルミート行列（自己随伴行列)

ユニタリ行列

正規行列

定理

定理1 転置行列について

定理2 行列の区分け

定理3 逆行列について

定理4

定理5

定理6 逆行列の存在の必要十分条件

定理7 ユニタリ変換の内積不変

定理8 ユニタリ行列の性質

用語

逆正弦

逆余弦

主値

符号関数

陰関数

代数関数

左極限

右極限

関数の連続性

偶関数

奇関数

凸関数

定理

定理2.1

定理2.2

定理2.3

定理2.4 中間値の定理

定理2.5 最大値の定理

用語

三角不等式

収束の定義

Cauchy列

上限,下限

実数の連続性の公理

交代級数

絶対収束

条件収束

各点収束

一様収束

関数級数

べき級数

収束半径

定理

定理1 （有界単調列の収束）

定理2 アルキメデスの原理

定理3 区間縮小法

定理4 ボルツァノ-ワイエルシュトラスの定理

定理5 が収束すれば、

定理6

定理7

定理10 はさみうちの原理

定理8 Cauchyの判定条件

定理9 コーシーの定理

定理10 級数に関するコーシーの定理

定理11

定理12

定理２　合成関数の微分

定理5 $\quad a_n, b_n$ が収束すれば、